“Sorting takes O(N log N).” We all know that.
But what if you don’t need everything sorted? What if you only care about the Top 10 users, or the Next urgent task?
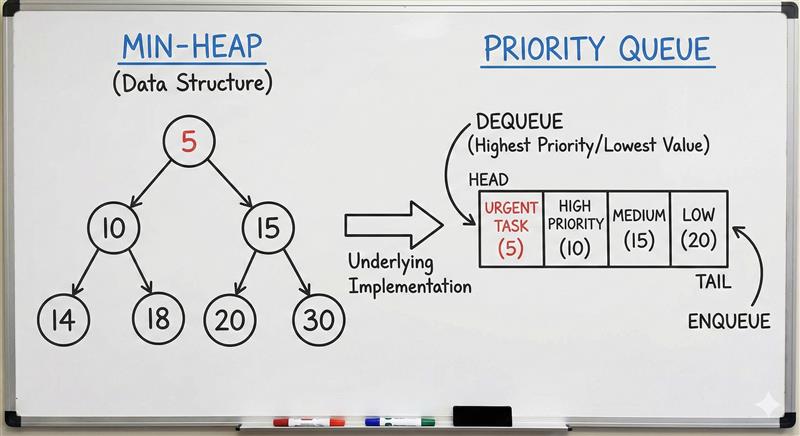
Sorting the whole dataset is a waste of resources. This is where the Heap (Priority Queue) shines. It allows us to extract the “Best” element in O(1) and insert a new one in O(log N). This is the backbone of operating systems, bandwidth management, and Dijkstra’s algorithm.
Here are the 7 Core Patterns you must master to crush the interview.
Part 1: The Basics (The “Tool” Knowledge)
Before you build, you must know your tools. C++ and Python are opposites here!
1. Min-Heap vs Max-Heap
- The Concept:
- Min-Heap: Parent < Children. Root is the Minimum.
- Max-Heap: Parent > Children. Root is the Maximum.
- The “Professor’s Warning”:
- C++ STL:
priority_queueis a Max-Heap by default. To make it Min, usegreater<int>. - Python:
heapqis a Min-Heap by default. To make it Max, multiply numbers by-1.
- C++ STL:
Part 2: The “Top K” Pattern (Selection)
The most common interview pattern. Stop sorting the whole array!
2. Top ‘K’ Elements (Static vs Stream)
- The Question: “Find the K largest elements in an array (or stream).”
- The Logic:
- Naive: Sort whole array O(N log N)
- Professor’s Method: Use a Min-Heap of size
K. - Iterate through data. Push to heap. If size > K, pop the smallest (root).
- At the end, the Heap contains the K largest elements.
- Complexity: O(N log K). (Huge improvement if K ll N).
3. K-Closest Points to Origin
- The Question: “Which K points are closest to (0,0)?”
- The Logic: Same strategy. Maintain a Max-Heap of size
Kbased on distance. - Why Max-Heap? Because to keep the closest (smallest distances), you need to kick out the farthest (largest distance) whenever the heap gets full.
Part 3: The “Merge” Pattern (External Sorting)
How databases sort Petabytes of data that don’t fit in RAM.
4. Merge K Sorted Lists
- The Question: “You have K sorted arrays. Merge them into one big sorted array.”
- The Logic:
- Push the first element of all
Karrays into a Min-Heap. - Pop the smallest (Root). Add to result.
- From the same array where that element came from, push the next element into the Heap.
- Push the first element of all
- Complexity: O(N log K) (where N is total elements).
Part 4: The “Median” Pattern (Two Heaps)
The “Goldman Sachs” Favorite.
5. Find Median from Data Stream
- The Question: “Numbers are coming in live. Tell me the Median at any second.”
- The Logic: A single heap can’t do this. You need Two Heaps.
- Max-Heap (Left): Stores the smaller half of numbers.
- Min-Heap (Right): Stores the larger half of numbers.
- Median: The top of the larger heap (or average of both tops).
- Complexity: Insert O(log N), Find Median O(1).
Part 5: The “Greedy” Heap Pattern
Using Heaps to make optimal decisions efficiently.
6. Connect Ropes / Minimum Cost
- The Question: “Connect N ropes with different lengths. Cost = Sum of lengths. Minimize total cost.”
- The Logic: Always connect the two smallest ropes first.
- Put all ropes in Min-Heap.
- Pop two, add them, push sum back.
- Repeat until one rope remains.
7. Task Scheduler / CPU Cooling
- The Question: “Schedule tasks (A, A, B…) such that same tasks are
nunits apart.” - The Logic:
- Count frequencies.
- Put tasks in a Max-Heap (do most frequent tasks first).
- Use a Queue to make them “wait” for
nseconds before pushing back to Heap.
The Professor’s Cheat Code Sheet
Stick this table at the bottom of your post. It clarifies the confusing “Min vs Max” choice.
| Problem Goal | Which Heap to Use? | Size of Heap | Time Complexity |
| Find K-Largest | Min-Heap | K | O(N log K) |
| Find K-Smallest | Max-Heap | K | O(N log K) |
| K-Closest Points | Max-Heap (Distance) | K | O(N log K) |
| Merge K Lists | Min-Heap (Values) | K | O(N log K) |
| Median of Stream | Max (Left) + Min (Right) | N/2 each | O(log N) |
| Task Scheduling | Max-Heap (Frequency) | 26 (constant) | O(N) |
| Sort Array | Max-Heap | N | O(N log N) |
Professor’s Advice for Teaching This
“Students, here is the secret:
- Don’t memorize the code. Memorize the Size limit.
- If I want the Top 10 guys, I maintain a VIP room of size 10.
- If a new guy enters, I compare him to the weakest guy in the room (Min-Heap root).
- If he is stronger, I kick the weak guy out.
That is the entire logic of Top-K. The rest is just syntax.”
The Complete Heap & Priority Queue Roadmap: 7 Algorithms from Beginner to Expert (2026 Guide)
Heap Data Structure Interview , Priority Queue C++ vs Python , Top K Elements Explanation , Merge K Sorted Lists Logic
YouTube Channels:
Trendy VS Vlogs
VS Coding Academy
Join Our WhatsApp Channel for the latest job opportunities and updates:
VS_CODING_ACADEMY WhatsApp Channel
Join Our Telegram Channel for the latest job opportunities and updates: https://t.me/vscodingacademy
Open our site in Telegram Bot: https://t.me/vscodingacademy_bot
For DSA Guide: https://vscodingacademy.com/category/dsa-guide/
